数据结构 有序数组表示稀疏矩阵

一般存储矩阵，自然想到二维数据。但是对于稀疏矩阵（0项很多），这无疑浪费的大量的空间。所以，这里考虑换一种表示方法。用一个三元组表示矩阵中的非零元素。

//(稀疏)矩阵数据结构, 待表示矩阵如下
// 15     0     0     22     0     -15
// 0     11     3     0     0     0
// 0     0     0     -6     0     0
// 0     0     0     0     0     0
// 91     0     0     0     0     0
// 0     0     28     0     0     0

#include <stdio.h>
#include <stdbool.h>
typedef struct {
     int col; // 列号
     int row; // 行号
     int value; // 值
} sparse_matrix;
void createMatrix(sparse_matrix *matrix);
void printMatrix(sparse_matrix *matrix);
void transposeMatrix(sparse_matrix *matrix, sparse_matrix *transposeMatrix);
#define GET_ARRAY_LEN(array,len) (len=(sizeof(array)/sizeof(array[0])));
int main() {   
     int length;
     sparse_matrix smatrix[9], transMatrix[9];
     createMatrix(smatrix);
     GET_ARRAY_LEN(smatrix,length);
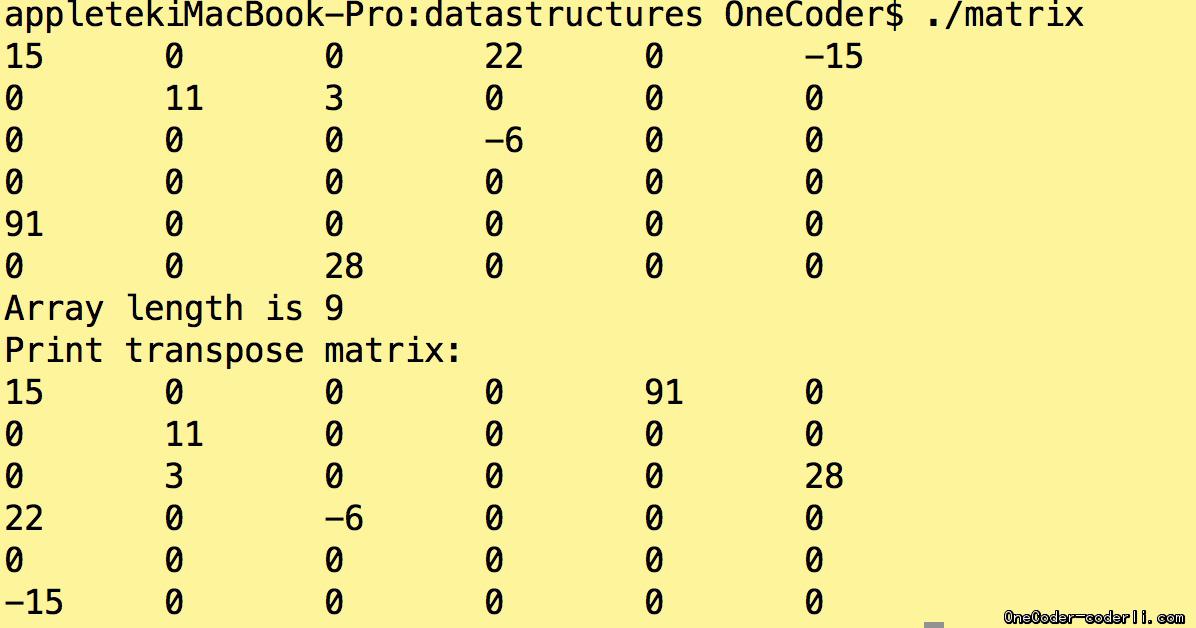
     printMatrix(smatrix);
     printf("Array length is %d\n",length);
     transposeMatrix(smatrix, transMatrix);
     printf("Print transpose matrix: \n");
     printMatrix(transMatrix);
    return 0;
}
// 初始化稀疏矩阵
void createMatrix(sparse_matrix *matrix) {
     matrix[0].row = 6;// 0行元素存储行数
     matrix[0].col = 6;// 0列元素存储列数
     matrix[0].value = 8;
     matrix[1].row = 0;
     matrix[1].col = 0;
     matrix[1].value = 15;
     matrix[2].row = 0;
     matrix[2].col = 3;
     matrix[2].value = 22;
     matrix[3].row = 0;
     matrix[3].col = 5;
     matrix[3].value = -15;
     matrix[4].row = 1;
     matrix[4].col = 1;
     matrix[4].value = 11;
     matrix[5].row = 1;
     matrix[5].col = 2;
     matrix[5].value = 3;
     matrix[6].row = 2;
     matrix[6].col = 3;
     matrix[6].value = -6;
     matrix[7].row = 4;
     matrix[7].col = 0;
     matrix[7].value = 91;
     matrix[8].row = 5;
     matrix[8].col = 2;
     matrix[8].value = 28;
}

//打印稀疏矩阵
//最差时间复杂度：O(row * col * valueCount);
void printMatrix(sparse_matrix *matrix) {
     int i,j,k;
     int row = (*matrix).row;
     int col = (*matrix).col;
     int valueCount = (*matrix).value;
     int startIndex = 1;
     for (i = 0; i < row; i++) {
          for (k = 0; k < col; k++) {
               bool print = false;
               for (j = startIndex; j <= valueCount; j++) {
                    int curRow = (*(matrix + j)).row,
                    curCol = (*(matrix + j)).col;
                    if (i == curRow && k == curCol) {
                         printf("%d\t", (*(matrix+j)).value);
                         print = true;
                         startIndex++;
                    }
               }
               if (!print) {
                    printf("%d\t", 0);
               }
          }
          printf("\n");
     }
}
// 求稀疏矩阵的转置矩阵，即交换行列的位置
// 最差时间复杂度：O(col * valueCount);
void transposeMatrix(sparse_matrix *smatrix, sparse_matrix *transposeMatrix) {
     int i,n, rowNum = (*smatrix).row, colNum = (*smatrix).col, valueNum = (*smatrix).value;
     (*transposeMatrix).row = colNum;
     (*transposeMatrix).col = rowNum;
     (*transposeMatrix).value = valueNum;
     int index = 1;
     for (i = 0; i < colNum; i++) {
          for (n = 1; n <= valueNum; n++) {
               int curRow = (*(smatrix + n)).row,
                    curCol = (*(smatrix + n)).col,
                    curValue = (*(smatrix + n)).value;
               if (i == curCol) {
                    (*(transposeMatrix + index)).row = curCol;
                    (*(transposeMatrix + index)).col = curRow;
                    (*(transposeMatrix + index)).value = curValue;
                    index++;
               }
          }
     }
}

可以看到，相对于传统的使用二维数据的方式存储矩阵，该存储方式对于稀疏矩阵来说，无疑节省了大量空间。  但是对于矩阵的打印和转置来说，从数据量级看浪费了时间。所以，此种表示方式适用于矩阵中非零元素少的稀疏矩阵。尤其当矩阵中非零元素数量为cols * rows时，转置的时间复杂性为O(rows * cols * cols)。用时间换空间。

考虑再用少量空间，换一些时间。实现时间复杂度的为O(cols + elements)的快速转置：

// 快速转置算法，浪费少量空间，换取时间
// 直接计算转置后元素的存放位置
void fastTranspose(sparse_matrix *smatrix, sparse_matrix *transposeMatrix) {
     int i, rowNum = (*smatrix).row, colNum = (*smatrix).col, valueNum = (*smatrix).value;
     int row_terms[colNum + 1],
          startPos[colNum + 1];
     (*transposeMatrix).row = colNum;
     (*transposeMatrix).col = rowNum;
     (*transposeMatrix).value = valueNum;
     for (i = 0; i< colNum; i++) {
          row_terms[i] = 0; // 数组中的元素必须初始化
     }
     for (i = 1; i <= valueNum; i++) {
          int     curCol = (*(smatrix + i)).col;
          row_terms[curCol]++;//记录转置后，每行的元素个数
     }
     startPos[0] = 1;//初始化起始位置
     for (i = 1; i < colNum; i++) {
          startPos[i] = startPos[i-1] + row_terms[i-1];
     }
      for (i = 1; i <= valueNum; i++) {
           int curRow = (*(smatrix + i)).row,
                curCol = (*(smatrix + i)).col,
                curValue = (*(smatrix + i)).value;
           int j = startPos[curCol]++;// 计算出原矩阵中的元素在转置矩阵数据中的位置
           (*(transposeMatrix + j)).row = curCol;
           (*(transposeMatrix + j)).col = curRow;
           (*(transposeMatrix + j)).value = curValue;
      }
}

可见快速转置的主要思想就是直接计算出元素在转置矩阵中的顺序位置，直接存储。接下来是稀疏矩阵的乘法。

// 稀疏矩阵乘法运算, 以下面矩阵为例
// 0     0     1     1 * 0     0
//                         0     0 = 2     5
//                         0     2
//                         2     3
void matrixMulti(sparse_matrix *amatrix, sparse_matrix *bmatrix, sparse_matrix *resultMatrix) {
     int i, aRowNum = (*amatrix).row, aValueNum = (*amatrix).value;
     int j, bColNum = (*bmatrix).col, bValueNum = (*bmatrix).value;
     (*resultMatrix).row = aRowNum;//首先可知结果矩阵的行列数
     (*resultMatrix).col = bColNum;
     sparse_matrix tbMatrix[9];// 为了计算方便先求出被乘矩阵的转置矩阵，下面计算都利用转置矩阵
     fastTranspose(bmatrix, tbMatrix);
         int temp_sum = 0,
          row = (*(amatrix + 1)).row, // 矩阵A的起始行，即为结果的起始行
          col,
          rowBegin = 1,
          rIndex = 0;
     // 在循环内部控制循环的次数和起始
     for (i = 1; i <= aValueNum; ) {
          col = (*(tbMatrix + 1)).row; // 矩阵B的转置矩阵的行，即对应的列
          for (j = 1; j <= bValueNum + 1; ) {
               if (amatrix[i].row != row) {
                    storeValue(resultMatrix, row, col, temp_sum, &rIndex);
                i = rowBegin;
                    for (; col == tbMatrix[j].row; j++)
                         ;
                    col = tbMatrix[j].row;
                    temp_sum = 0;
               } else if (col != tbMatrix[j].row) {
                    storeValue(resultMatrix, row, col, temp_sum, &rIndex);
                i = rowBegin;
                col = tbMatrix[j].row;
                    temp_sum = 0;
               } else {
                    if (amatrix[i].col < tbMatrix[j].col) {
                         i++;
                    } else if (amatrix[i].col == tbMatrix[j].col) {
                         temp_sum += amatrix[i].value * tbMatrix[j].value;
                         i++;
                         j++;
                    } else {
                         j++;
                    }
               }
          }
          for (; row == (*(amatrix + i)).row; i++)
               ;
          rowBegin = i;
          row = (*(amatrix + i)).row;
     }
    (*resultMatrix).value = rIndex;
}

void storeValue(sparse_matrix *resultMatrix, int row, int col, int value, int *index) {
     if (value) {
          (*(resultMatrix + ++*index)).row = row;
          (*(resultMatrix + *index)).col = col;
          (*(resultMatrix + *index)).value = value;
     }
}

没有做太多错误边界的判断。计算结果：

初学乍练，如果有错误还望大家指出。这个乘法，OneCoder着实写了好久。算法的时间复杂度为：O(bColNum * aValueNum + aRowNum * bValueNum)。相对于传统的二维数组表示矩阵的计算来说，实现逻辑复杂好多。传统方式的时间复杂度为：O(aRowNum * aColNum * bColNum)。