【GESP】C++一级练习BCQM3009，简单二进制字符串输出

一道简单的二进制字符串输出题。初识二进制数字规律，人肉计算后输出。

BCQM3009

题目要求

描述

对于长度为 3位的一个 0、1 串，每一位都可能是 0 或 1 ，一共有 8 种可能。它们的前几个是：

000
001
010
……

请按从小到大的顺序输出这 8种 01串。

输入

无

输出

输出 8行，按从小到大的顺序每行一个长度为 3 的 01 串。

输入样例

无

输出样例

000
001
010
011
100
101
110
111

题目分析

题目在语法上没有难度，就是输出一个二进制字符串。对于程序初学者(甚至小学生而言)如果没有输出样例做“参考”，那你需要自己掌握二进制的计数规律。这里插入一段初学者二进制科普。

---

初学者二进制科普

（1）什么是二进制？

1. 二进制是一种只用两个数字——0和1——来表示所有内容的数字系统。
2. 我们平常用的十进制系统有10个数字：0到9。二进制系统只有两个数字：0和1，所以叫二进制。

（2）为什么用二进制？

1. 计算机是由许多小开关组成的，每个开关只有两个状态：
   • 开 = 1
   • 关 = 0
2. 二进制非常适合用来表示这些状态。通过许多0和1的组合，计算机可以表示任何数字、文字和图片！就像用积木可以搭出很多不同的形状，二进制的0和1也可以组合出无穷多的可能性。

（3）如何用二进制表示数字？

为了帮助初学者和小学生理解二进制和十进制数数的区别，我们可以通过将两者并列展示，让他们清晰地看到每次进位的变化。

数数方式对比：

十进制：

• 从0开始：每次加1。
• 当个位满9时，再加1就会进到下一位。例如：9 + 1 = 10。

二进制：

• 从0开始：每次也是加1，但每位数只有0和1。
• 当某一位满1时，加1就会进位，因为1之后没有别的数字了。例如，
  • 1 + 1 = 10（表示“2”），就像十进制里的9之后变为10。
  • 11 + 1 = 100（表示“4”）

根据上述规律，列出0-10的二进制表示对比，加深理解：

十进制（我们平常用的）	二进制（计算机用的）
0	0
1	1
2	10
3	11
4	100
5	101
6	110
7	111
8	1000
9	1001
10	1010

---

（4）二进制和十进制的转换

• 我们平常用的十进制是基于10的。举个例子，数字345表示：
  • 3在百位（3×10^2 = 300）
  • 4在十位（4×10^1 = 40）
  • 5在个位（5×10^0 = 5）

  结果：300 + 40 + 5 = 345。

• 而二进制是基于2的。例如二进制101表示：
  • 1在4位（1×2^2 = 4）
  • 0在2位（0×2^1 = 0）
  • 1在1位（1×2^0 = 1）

  结果：4 + 0 + 1 = 5，所以二进制的101等于十进制的5。

（5）更多例子

我们来看更大的数：二进制：1011

• 从右到左，第一位是1，代表2^0 = 1，值为1×1 = 1。
• 第二位是1，代表2^1 = 2，值为1×2 = 2。
• 第三位是0，代表2^2 = 4，值为0×4 = 0。

• 第四位是1，代表2^3 = 8，值为1×8 = 8。

  最终：8 + 0 + 2 + 1 = 11，所以二进制的1011等于十进制的11。

总结

1. 从右往左数，每一位表示2的幂次方（从2^0开始）。
2. 如果该位是1，就把对应的2的幂次方加起来；如果是0，就跳过那一位。
3. 把所有结果加在一起，得到十进制数字。

---

回到题目，按照二进制计数规律，输出000-111即可。

代码参考

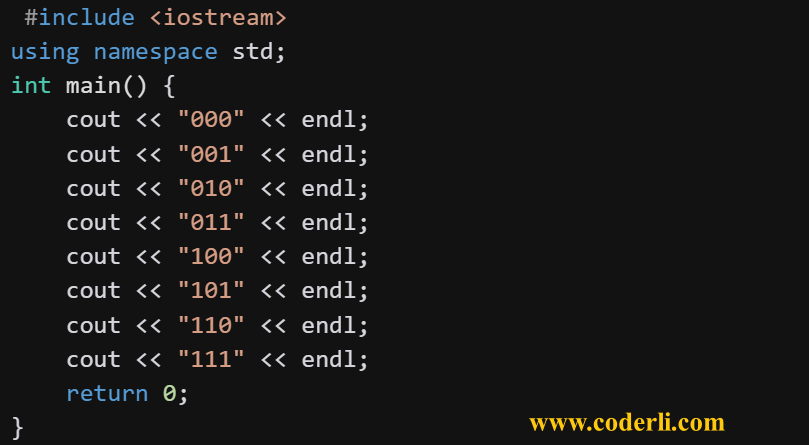
 #include <iostream>
using namespace std;
int main() {
    cout << "000" << endl;
    cout << "001" << endl;
    cout << "010" << endl;
    cout << "011" << endl;
    cout << "100" << endl;
    cout << "101" << endl;
    cout << "110" << endl;
    cout << "111" << endl;
    return 0;
}

所有代码已上传至Github：https://github.com/lihongzheshuai/yummy-code